Jawaban Soal latihan 1.1 Matematika Kelas 12 Halaman 12

Soal Latihan 1.1 Matematika Kelas 12

SMA/SMK/MAK

Halaman: 12

BAB 1 (Dimensi 3)

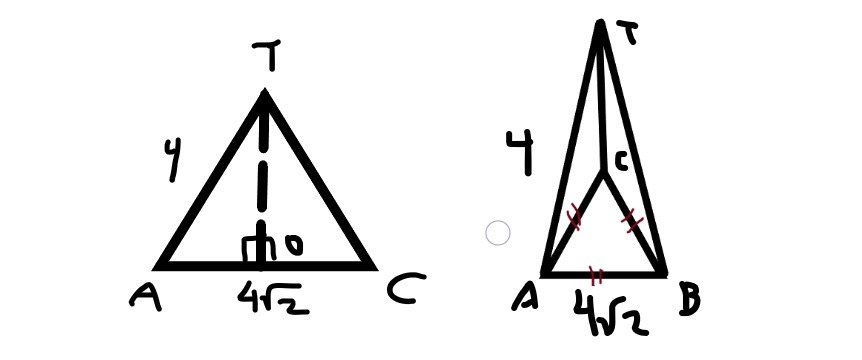
1. Diketahui limas beraturan T.ABC dengan bidang alas berbentuk segitiga
sama sisi. TA tegak lurus dengan bidang alas. Jika panjang AB = 4 cm dan TA = 4 cm, tentukan jarak antara titik T dan C!
Jawab:
Dik: limas T.ABC alas segitiga sama sisi,
TA tegak lurus bidang alas.
AB = 4(2)^1/2 cm dengan TA = 4cm,
Dit: TC = ?

$4 = \sqrt{ 2\sqrt{2}^{2} + TO^{2} } \\ 16 = 8 + TO^{2} \\ TO = \sqrt{8} \\ TO = 2\sqrt{2}$

$TC = \sqrt{\frac{AC}{2}^{2} + TO^{2}} \\ TC = \sqrt{2\sqrt{2}^{2} + (2\sqrt{2}^{2}) } \\ TC = \sqrt{8 + 8} \\ TC = 4 cm$

2. Perhatikan limas segi enam beraturan berikut

Diketahui panjang AB = 10 cm dan TA = 13 cm. Titik O merupakan titik tengah garis BE. Tentukan jarak antara titik T dan O!

Jawab:
Dik: limas segienam T.ABCDEF
AB = 10 cm
TA = 13 cm .
Titik O merupakan titik tengah garis BE .
Dit : jarak antara titik T dan O :
perhatikan alas limasnya, alas limas berbentuk segi 6 beraturan, jika kita ambil 1 segitiga akan membentuk segitiga sama sisi,
sehingga BO = AB = 10 cm
TB = TA = 13 cm

perhatikan segitiga BTO
segitiga BTO segitiga siku" di O
segingga panjang TO bisa kita hitung dengan menggunakan pythagoras

TO = √(13² - 10²)
= √(169 - 100)
= √69 cm
jadi jarak antara titik T ke titik O = √69 cm

Baca Juga :

3. Perhatikan bangun berikut ini.

Jika diketahui panjang AB = 5 cm, AE = BC = EF = 4 cm, maka tentukan:
a. Jarak antara titik A dan C
b. Jarak antara titik E dan C
c. Jarak antara titik A dan G

Jawab:

a. Untuk menjawab soal ini silahkan lihat gambar terlampir, untuk mencari besar AC, kita tentukan dulu AB dan BC, diketahui AB = 5 cm dan CB = 4cm, maka

AC^2 = AB^2 + CB^2

AC^2 = 5^2 + 4^2

maka AC = (41)^1/2 cm

b. Untuk mencari besar EC, tentukan dulu panjang AE dan AC. Diketahui panjang AE = 4 cm, dan AC = (41)^1/2 cm maka:

EC^2 = AE^2 + AC^2

EC^2 = 4^2 + 41

EC^2 = 16 + 41

EC = (57)^1/2 cm

c. Untuk mencari besar AG tentukan dulu panjang AH dan HG. Diketahui panjang AH = 4.(2)^1/2 cm dimana

AH didapat dari

AH^2 = AD^2 + DH^2

AH^2 = 4^2 + 4^2