Uji Kompetensi 5
Bab 5 Perbandingan
Halaman 58-62
B. Soal Uraian
Matematika (MTK)
Kelas 7 SMP/MTS
Semester 2 K13
Perhatikan tabel di bawah ini.
Persentase Akses Air Minum Layak Rumah Tangga di Indonesia
a. Bandingkan persentase akses air minum layak perkotaan terhadap pedesaan dan persentase akses air minum layak pedesaan terhadap perkotaan. Tulislah pernyataan untuk masing-masing tahun.
b. Jelaskan kenaikan atau penurunan akses air minum layak di perkotaan dan di pedesaan antara tahun 2000 dan 2011.
Penyelesaian:
a.
Pada tahun 2000, persentase akses air minum layak perkotaan (46,02 %) lebih tinggi dari pada persentase akses air minum layak pedesaan (31,31%).
Pada tahun 2011, persentase air minum layak pedesaan (43,92%) lebih tinggi dari pada persentase akses air minum layak di perkotaan (41,10%).
b.
Penurunan persentase akses air minum perkotaan = 46,02% - 41,10% = 4,92%
Kenaikan persentase akses air minum pedesaan = 43,92% - 31,31% = 12,61%
__________________________
2. Ratna ingin membeli mi instan. Ratna memiliki dua pilihan tempat untuk membeli mi instan. Di AndaMart, Ratna dapat membeli tujuh bungkus mi instan seharga Rp13.000,00. Sedangkan di SandiMart, Ratna dapat membeli enam bungkus mi instan seharga Rp11.000,00. Toko manakah yang akan kalian sarankan ke Ratna? Jelaskan.
Penyelesaian:
Toko Andamart
7 bungkus = Rp 13.000,00
1 bungkus = Rp 1.857,14286
Toko Sandimart
6 bungkus = Rp 11.000,00
1 bungkus = Rp 1.833,33333
Harga 1 bungkus mie lebih murah di toko Sandimart, jadi lebih baik beli mie di toko Sandimart
__________________________
Penyelesaian:
Jarak A dan B pada peta = 6 cm
Jarak A dan B sebenarnya = 120 km = 12.000.000 cm
Skala = jarak pada peta : jarak sebenarnya = 6 : 12.000.000 = 1 : 2.000.000
Jarak B dan C pada peta = 4 cm
Skala = 1 : 2.000.000 =
Jarak sebenarnya = Jarak pada peta : skala = 4 :
Jadi, jarak sebenarnya dari kota B ke kota C adalah 80 km.
__________________________
Penyelesaian:
Rasio = r
r1 = a
r2 = b
a = 3/4 b
a + 2 = 7/9 (b + 2)
3 b / 4 + 2 = 7/9 (b + 2)
27b/ 4 + 18 = 7b + 14
7b - 27b/4 = 18 - 14
(28b - 27b)/4 = 4
b/4 = 4
b = 16
a = 3/4 . 16
a = 3 . 4 = 12
hasil kali
= a . b
= 12 . 16
= 192
__________________________
Berikut ini sebaran titik koordinat yang menunjukkan jarak (d) terhadap waktu (t). Variabel d dalam satuan meter dan variabel t dalam satuan detik. Grafik tersebut menjelaskan seseorang berjalan dari detektor gerakan.
a. Taksirlah seberapa cepat orang ini bergerak. Jelaskan bagaimana kamu mengetahuinya.
b. Buatlah tabel yang taksirannya sama dengan grafik di samping.
c. Apakah sebaran plot ini menunjukkan perbandingan senilai atau berbalik nilai? Jelaskan.
d. Tentukan persamaan dari perbandingan jarak terhadap waktu berdasarkan grafik di samping.
Penyelesaian:
Jika waktu (t) = 2 detik (dt) dan jarak (s) = 2 meter (m), maka kecepatan (v) = s/t = 2/2 = 1 m/dt, kemudian waktu (t) = 3 detik (dt) dan jarak (s) = 3 meter (m), maka kecepatan (v) = 3/3 = 1 m/dt dan seterusnya.
Tabel yang menggambarkan grafik pada gambar lampiran, yaitu :
jarak (s) dalam meter (m) waktu (t) dalam detik (dt)
0,5 0,5
1 1
1,5 1,5
2 2
2,5 2,5
3 3
3,5 3,5
4 4
dan seterusnya.
Bila kita perhatikan tabel dan definisi tentang perbandingan senilai, maka sebaran plot pada gambar grafik terlampir termasuk perbandingan senilai.
Persamaan dari grafik pada gambar terlampir, yaitu :
t/t₁ = s/s₁
misalnya kita ambil satu titik (2, 2) dengan t₁ = 2 dan s₁ = 2, maka
⇔t/2 = s/2
⇔t = 2s/2
⇔t = s
Untuk titik-titik yang lain persamaan dari grafik tersebut sama.
__________________________
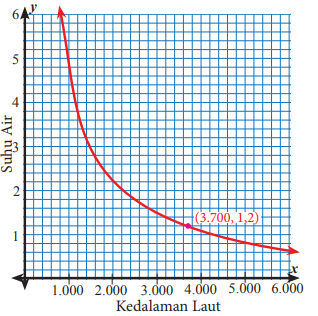
Grafik di bawah menunjukkan suhu air di Samudera Pasifik. Asumsikan suhu dan kedalaman laut berbanding terbalik pada kedalaman yang lebih dari 900 meter.
a. Tentukan persamaan yang berhubungan dengan suhu T dan kedalaman laut m.
b. Tentukan suhu pada kedalaman 5.000 meter.
Penyelesaian:
 __________________________
__________________________Gambar di atas menunjukkan jejak kaki seorang pria yang berjalan. Panjang langkah P adalah jarak antara dua ujung belakang jejak kaki yang berurutan.
Untuk pria, rumus n/p = 140 , menunjukkan hubungan antara n dan P dimana n menunjukkan banyak langkah per menit, dan P menunjukkan panjang langkah dalam satuan meter.
a. Jika rumus di atas menunjukkan langkah kaki Heri dan dia berjalan 70 langkah per menit, berapakah panjang langkah Heri? Tunjukkan bagaimana kalian menentukannya.
b. Beni mengetahui bahwa panjang langkah kakinya adalah 0,80 meter. Jika rumus tersebut menunjukkan langkah kaki Beni, hitung kecepatan Beni berjalan dalam meter per menit dan dalam kilometer per jam.Tunjukkan strategi kalian menyelesaikannya.
Penyelesaian:
 __________________________
__________________________Mei Ling dari Singapura sedang mempersiapkan kepergiannya ke Afrika Selatan selama 3 bulan dalam pertukaran pelajar. Dia harus menukarkan uang Dolar Singapura (SGD) miliknya menjadi Rand Afrika Selatan (ZAR).
a. Mei Ling mengecek nilai tukar uang asing antara Dolar Singapura dan Rand Afrika Selatan, yakni 1 SGD = 4,2 ZAR. Mei Ling menukar 3.000 dolar Singapura menjadi Rand Afrika Selatan sesuai nilai tukar tersebut.
Berapakah uang yang diperoleh Mei Ling dalam Rand Afrika Selatan ?
b. Ketika kembali ke Singapura selama 3 bulan, uang Mei Ling bersisa 3.900 ZAR. Dia menukarkannya menjadi Dolar Singapura, perhatikan bahwa nilai tukar kedua mata uang tersebut telah berubah menjadi 1 SGD = 4,0 ZAR.
Berapakah uang yang didapatkan Mei Ling setelah ditukarkan menjadi Dolar Singapura?
c. Selama 3 bulan nilai tukar mata uang asing telah berubah mulai 4,2 menjadi 4,0 ZAR per SGD. Apakah hal ini keberuntungan yang didapatkan Mei Ling bahwa nilai tukar sekarang yang sebelumnya 4,0 menjadi 4,2 ZAR, ketika dia menukar ZARnya menjadi SGD? Berikan penjelasan untuk mendukung jawabanmu.
Penyelesaian:
A. 1sgd = 4,2 zar
3000 sgd = 3000x4,2 zar
3000 sgd= 12600 zar
b. 1 sgd = 4 zar
3900 zar = 3900:4
3900 zar = 925 sgd
c. ya, keberuntungan mei ling karena jumlah uang zar yang ia tukar dengan sgd menjadi lebih banyak
__________________________
Hubungan antara ukuran katrol dan kecepatan berputar berbanding terbalik. Katrol seperti gambar di atas. Diameter katrol A dua kali diameter katrol B. Sehingga, jika katrol A berputar sekali, katrol B berputar dua kali. Misalkan katrol A berdiameter tiga kali katrol B, maka ketika A berputar sekali, katrol B berputar tiga kali. Diameter katrol B yang lebih kecil dibandingkan dengan diameter katrol A. Kecepatan putaran katrol berbanding terbalik terhadap diameter. Kita dapat menyatakannya dalam persamaan berikut.
R-k/d, dimana R adalah kecepatan katrol dalam revolusi per menit (rpm) dan d adalah diameter katrol.
a. Katrol A diputar terhadap katrol B. Katrol B berdiameter 40 cm dan berotasi 240 rpm. Tentukan kecepatan katrol A jika diameternya 50 cm.
b. Katrol B diputar terhadap katrol A. Katrol A berdiameter 30,48 cm dan berkecepatan 300 rpm. Katrol B berdiameter 38,1 cm. Berapakah kecepatan yang dihasilkan oleh katrol B?
c. Katrol pada sebuah mesin berdiameter 9 inci dan berputar 1260 rpm. Katrol ini diikat sabuk karet dengan katrol yang lebih kecil pada motor elektrik. Katrol yang kecil berdiameter 5 inci. Tentukan kecepatan katrol yang kecil.
d. Apakah keliling lingkaran (katrol) berbanding lurus dengan diameternya? Jelaskan.
e. Bagaimanakah keliling lingkaran berpengaruh jika diameternya dilipatgandakan?
Penyelesaian:

 __________________________
__________________________a. Buatlah tabel nilai yang mungkin untuk x dan y jika luas persegipanjang adalah 12 m2. Kemudian dari tabel yang kalian buat, gambarkan grafiknya.
b. Apakah hubungan x dan y senilai, berbalik nilai, atau bukan keduanya? Jelaskan alasan kalian.
c. Buatlah tabel nilai yang mungkin untuk x dan y jika luas persegipanjang adalah 12 m2. Kemudian dari tabel yang kalian buat, gambarkan grafiknya dengan menggunakan bidang koordinat yang sama pada soal a).
d. Bagaimanakah hubungan luas persegipanjang pertama dengan luas persegipanjang yang kedua? Jika nilai x yang diketahui, bagaimanakah hubungan antara nilai y pada persegipanjang pertama dan nilai y pada persegipanjang kedua? Jika nilai y yang diketahui, bagaimanakah hubungan antara nilai x pada persegipanjang pertama dan nilai x pada persegipanjang kedua?
Penyelesaian:
 __________________________
__________________________