Kunci Jawaban MTK Kelas 8 Halaman 11 Ayo Kita Berlatih 6.1

Berikut ini merupakan pembahasan kunci jawaban Buku MTK untuk Kelas 8 halaman 11. Pembahasan kali ini kita akan bahas latihan yang ada pada bab 6 Teorema Pythagoras. Ayo Kita Berlatih 6.1 hal 11 - 13, buku siswa untuk semester 2 Kelas VIII. Semoga dengan adanya pembahasan kunci jawaban ayo berlatih 6.1 Matematika kelas 8 ini, kalian bisa menjadi lebih giat untuk belajar. Kunci jawaban ini diperuntukkan untuk para pelajar yang sedang mengerjakan tugas.

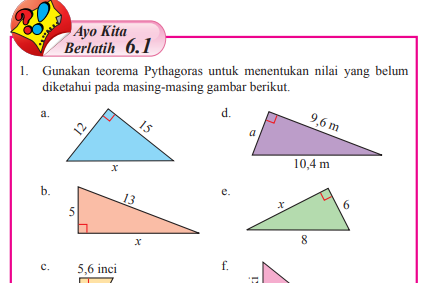
1. Gunakan teorema Pythagoras untuk menentukan nilai yang belum diketahui pada masing-masing gambar berikut.

Jawaban :

a)
x = √(122 + 152)
= √(144 + 225)
= √369

b)
x = √(132 - 52)
= √(169 - 25)
= √144
= 12

c)
a = √(10,62 - 5,62)
= √(112,36 - 31,36)
= √81
= 9 inchi

d)
a = √(10,42 - 9,62)
= √(108,16 - 92,16)
= √16
= 4 m

e)
x = √(82 - 62)
= √(64 - 36)
= √28

f)
a = √(7,22 + 9,62)
= √(51,84 + 92,16)
= √144
= 12 kaki

2. Tujuan dipasangkan kawat bubut pada suatu tiang telepon adalah untuk menopangnya. Kawat bubut dipasang pada tiang telepon setinggi 8 meter dari tanah.

a. Jelaskan cara yang akan kalian lakukan untuk menentukan panjang kawat bubut tanpa mengukur langsung kawat tersebut.

b. Tentukan panjang kawat jika jarak antara kawat dan tiang pada tanah adalah 6 meter

Jawaban :

a) Caranya dengan mengukur jarak antara kawat dengan tiang lalu, Dengan menggunakan rumus Teorema Pythagoras kita dapat mencari panjang kawat bubut,

b)
kawat = √(jarak2 + tinggi2)
= √(62 + 82)
= √(36 + 64)
= √100
= 10 m
Jadi, panjang kawat bubut tersebut adalah 10 meter.

3. Tentukan nilai x pada kedua gambar berikut.

Jawaban :

Bangun I )
x = √(Sisi miring2 - Sisi tegak2)
= √(202 - 122)
= √(400 - 144)
= √256
= 16 cm
Jadi, panjang x adalah 16 cm.

Bangun II )
Cari nilai y terlebih dahulu,
y = √(132 - 52)
= √(169 - 25)
= √144
= 12 mm
x = √(y2 + 352)
= √(122 + 352)
= √(144 + 1225)
= √1369
= 37 mm
Jadi, panjang x adalah 37 mm.

4. Apakah suatu segitiga yang panjang ketiga sisinya berturut-turut 9 cm,12 cm, dan 18 cm merupakan segitiga siku-siku? Jelaskan.

Jawaban :

Kita dapat menggunakan Teorema Pythagoras, dengan rumus :
sisi paling panjang kuadrat = sisi 1 lainnya kuadrat + sisi 2 lainnya kuadrat
182 = 92 + 122
324 = 81 + 144
324 = 225 (salah)

Jadi, jawabannya adalah salah karena tidak memenuhi kriteria Teorema Pythagoras.

5. Jika panjang sisi-sisi suatu segitiga siku-siku berturut-turut adalah x, 15, dan x + 5, tentukan nilai x.

Jawaban :

Dengan menggunakan pythagoras maka,
x² + 15² = (x + 5)²
x² + 225 = x² + 10x + 25
x² - x² - 10x = 25 - 225
-10x = -200
x = -200 / -10
x = 20

Jadi, nilai x adalah 20.

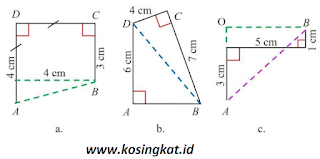
6. Tentukan panjang AB dari gambar berikut.

Jawaban :

*Perhatikan Ilustrasi Gambar diatas*

a)
AB = √(CD² + (AD - BC)²)
= √(4² + (4 - 3)²)
= √(16 + 1)
= √17 cm
Jadi, panjang AB adalah √17 cm.

b)
BD = √(BC² + CD²)
= √(7² + 4² BD²)
= √(49 + 16)
= √65

AB² = √(BD² - AD²)
= √((√65)² - 6²)
= √(65 - 36)
= √29 cm
Jadi, panjang AB adalah √29 cm.

c)
AB = √(AO² + BO²)
= √(4² + 5²)
= √(16 + 25)
= √41 cm
Jadi, panjang AB adalah √41 cm.

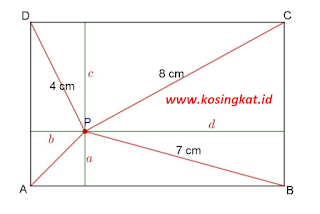
7. Diketahui persegi panjang ABCD dan P merupakan titik di dalam persegi panjang. Jika PC = 8 cm, PD = 4 cm, dan PB = 7 cm, maka PA adalah ..

Jawaban :

*Perhatikan ilustrasi gambar diatas*

PA = √(PD² + PB² - PC²)
= √(4² + 7² - 8²)
= √(16 + 49 - 64)
= √(65 - 64)
= √1
= 1 cm
Jadi, panjang PA adalah 1 cm.

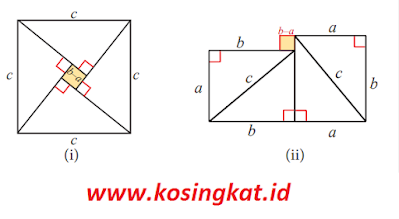
8. Seorang yang bernama Bhaskara menyusun sebuah persegi dan empat buah segitiga siku-siku yang memiliki panjang sisi yang sama yaitu a, b dan c kedalam sebuah persegi yang mempunyai panjang sisi c.

Jawaban :

a) Kelima potongan bangun datar tersebut akan membentuk bangun yang paling kanan seperti pada gambar dibawah ini.

b)
Pada gambar (i) terlihat bahwa Luas persegi besar adalah c2.
Dengan menggunakan penjumlahan luas beberapa bangun pada gambar (ii), sehingga akan terbukti bahwa c2 = a2 + b2.
Luas bangun (ii) adalah
2 × (ab) + (b – a)2 = 2ab + b2 –2ab + a2 = a2 + b2

Jadi, karena luas bagun pada gambar (i) sama dengan luas bangun (ii), maka terbukti benar bahwa teorema Pythagoras berlaku.

9. Perhatikan gambar dua persegi di samping. Panjang sisi persegi besar adalah 15 cm. Luas persegi kecil adalah 25 cm2 . Tentukan nilai x.

Jawaban :

Karena kedua bangun tersebut merupakan persegi maka memiliki panjang sisi yang sama.
Panjang sisi bangun (i) = 15 cm
Panjang sisi bangun (ii) = √25 = 5 cm
Sehingga akan diperloeh,
AB = 15 cm
BC = 15 + 5 = 20 cm
Dengan menggunakan pythagoras kita dapat menemukan nilai x.
x = √(AB2 + BC2)
= √(152 + 202)
= √(225 + 400)
= √625
= 25 cm

Jadi, nilai x adalah 25 cm.

10. Perhatikan gambar di samping. Diketahui ∆ABC siku-siku di B dengan panjang AC = 40 cm dan BC = 24 cm. Titik D terletak pada AB sedemikian sehingga CD = 25 cm. Panjang AD = ... cm.

kunci jawaban ayo kita berlatih 6.1 matematika kelas 8 semester 2 halaman 12, 13

Jawaban :

AC = 40 cm
BC = 24 cm
CD = 25 cm
AD = AB - DB

Langkah 1 Cari panjang AB :
AB = √(AC2 - BC2)
= √(402 + 242)
= √(1600 - 576)
= √1024
= 32 cm

Langkah 2 Cari panjang DB :
DB = √(CD2 - BC2)
= √(252 - 242)
= √(625 - 576)
= √49
= 7 cm

AD = AB - DB
= 32 - 7
= 25 cm

Jadi, panjang AD adalah 25 cm.

Baca Selanjutnya :

Kunci Jawaban MTK Kelas 8 Halaman 11 Ayo Kita Berlatih 6.1

Kunci Jawaban MTK Kelas 8 Halaman 11 Ayo Kita Berlatih 6.1

Related Posts