 |
| Kunci Jawaban MTK Kelas 10 Halaman 126 Uji Kompetensi 4.1 |
Kunci Jawaban MTK Kelas 10 Halaman 126 Uji Kompetensi 4.1
Uji Kompetensi 4.1
1. Tentukan nilai kebenaran (benar atau salah) setiap pernyataan di bawahini. Berikan penjelasan untuk setiap jawaban yang diberikan.
Jawaban :
a) Benar;
b) Salah;
c) Salah;
d) Salah;
e) Benar;
a) Benar;
b) Salah;
c) Salah;
d) Salah;
e) Benar;
2. Diketahui besar sudut a kurang dari 90° dan besar sudut θ lebih dari atau sama dengan 90° dan kurang dari 180°. Analisislah kebenaran setiap pernyataan berikut ini.
Jawaban :
a) Terdapat besaran α yang kurang dari 90°, misalnya untuk α = 15°, sedemikian sehingga
2 x α = 2 x 15° = 30° < 90°.
Jadi, pernyataan tersebut bernilai salah.
b) Terdapat besaran α yang kurang dari 90°, misalnya α = 75° dan besaran θ yang lebih dari atau sama dengan 90° dan kurang dari 180°,misalnya θ = 95°, sedemikian sehingga θ – α = 95° – 75° = 20° < 30°.
Jadi, pernyataan tersebut bernilai salah.
c) Terdapat besaran α yang kurang dari 90°, misalnya α = 10° dan besaran θ yang lebih dari atau sama dengan 90° dan kurang dari 180°, misalnya θ = 100°, sedemikian sehingga
2α + 1/2 θ = 2 x 10° + 1/2 x 100°
= 20° + 50° = 70° < 90°
Jadi, pernyataan tersebut bernilai salah.
d) Persamaan 2θ – 2α = θ + α ⇔ θ = 3α. Jadi, dapat dipilih α = 30° dan θ = 15° sedemikian sehingga 150° atau θ = 3α
Jadi, pernyataan tersebut bernilai benar.
a) Terdapat besaran α yang kurang dari 90°, misalnya untuk α = 15°, sedemikian sehingga
2 x α = 2 x 15° = 30° < 90°.
Jadi, pernyataan tersebut bernilai salah.
b) Terdapat besaran α yang kurang dari 90°, misalnya α = 75° dan besaran θ yang lebih dari atau sama dengan 90° dan kurang dari 180°,misalnya θ = 95°, sedemikian sehingga θ – α = 95° – 75° = 20° < 30°.
Jadi, pernyataan tersebut bernilai salah.
c) Terdapat besaran α yang kurang dari 90°, misalnya α = 10° dan besaran θ yang lebih dari atau sama dengan 90° dan kurang dari 180°, misalnya θ = 100°, sedemikian sehingga
2α + 1/2 θ = 2 x 10° + 1/2 x 100°
= 20° + 50° = 70° < 90°
Jadi, pernyataan tersebut bernilai salah.
d) Persamaan 2θ – 2α = θ + α ⇔ θ = 3α. Jadi, dapat dipilih α = 30° dan θ = 15° sedemikian sehingga 150° atau θ = 3α
Jadi, pernyataan tersebut bernilai benar.
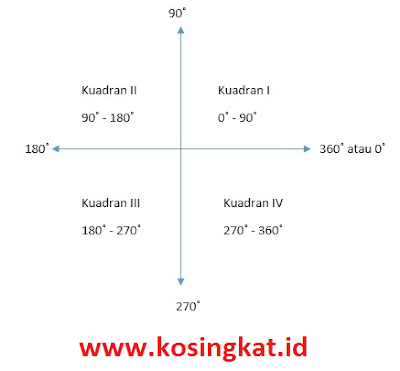
3. Berikut ini merupakan besar sudut dalam satuan derajat, tentukan kuadran setiap sudut tersebut.
a. 90°
b. 135°
c. 225°
d. 800°
e. –270°
f. 1.800°
Selanjutnya, nyatakan setiap sudut di atas dalam satuan radian.
Jawaban :
Kuadran I : 0 < α < 1/2 π
Kuadran II : 1/2 π < α < π
Kuadran III : π < α < 3/2 π
Kuadran IV : 3/2 π < α < 2π
a. Batas Kuadran; 1/2 π
b. Kuadran II; 3/4 π
c. Kuadran III; 5/4 π
d. Kuadran; 4/9 π
e. Batas Kuadran II; - 3/2 π
f. Batas Kuadran I; 10Ï€
Kuadran I : 0 < α < 1/2 π
Kuadran II : 1/2 π < α < π
Kuadran III : π < α < 3/2 π
Kuadran IV : 3/2 π < α < 2π
a. Batas Kuadran; 1/2 π
b. Kuadran II; 3/4 π
c. Kuadran III; 5/4 π
d. Kuadran; 4/9 π
e. Batas Kuadran II; - 3/2 π
f. Batas Kuadran I; 10Ï€
4. Tentukan (dalam satuan derajat dan radian) untuk setiap rotasi berikut.
Jawaban :
a)
1/9 putaran x 360° = 40°
1/9 putaran x 2Ï€ rad = 2Ï€/9 rad
b)
3/8 putaran x 360° = 135°
3/8 putaran x 2Ï€ rad = 3Ï€/4 rad
c)
1/5 putaran x 360° = 72°
1/5 putaran x 2Ï€ rad = 2Ï€/5 rad
d)
9/8 putaran x 360° = 405°
9/8 putaran x 2Ï€ rad = 9Ï€/4 rad
e)
3/4 putaran x 360° = 270°
3/4 putaran x 2Ï€ rad = 3Ï€/2 rad
f)
7/6 putaran x 360° = 420°
7/6 putaran x 2Ï€ rad = 7Ï€/3 rad
a)
1/9 putaran x 360° = 40°
1/9 putaran x 2Ï€ rad = 2Ï€/9 rad
b)
3/8 putaran x 360° = 135°
3/8 putaran x 2Ï€ rad = 3Ï€/4 rad
c)
1/5 putaran x 360° = 72°
1/5 putaran x 2Ï€ rad = 2Ï€/5 rad
d)
9/8 putaran x 360° = 405°
9/8 putaran x 2Ï€ rad = 9Ï€/4 rad
e)
3/4 putaran x 360° = 270°
3/4 putaran x 2Ï€ rad = 3Ï€/2 rad
f)
7/6 putaran x 360° = 420°
7/6 putaran x 2Ï€ rad = 7Ï€/3 rad
5. Nyatakan dalam radian besar sudut yang dibentuk untuk setiap penunjukan waktu berikut.
Jawaban :
a) Jam 12.05
Pergerakan jarum pendek = 5 menit
= 5/60 × 30⁰
= 2,5⁰
Pergerakan jarum panjang = 5 menit
= 5/60 × 360⁰
= 30⁰
Sudut yang terbentuk = 30 - 2,5⁰
= 27,5⁰
= 27,5⁰ x Ï€/180⁰ Ï€ rad
= 11Ï€/72 rad
Dengan mengikuti langkah diatas maka akan didapatkan jawaban untuk pertanyaan lainnya,
b)11Ï€/24 rad
c) 343Ï€/360 rad
d) 109Ï€/120 rad
e) 61Ï€/120 rad
f) π/4 rad
a) Jam 12.05
Pergerakan jarum pendek = 5 menit
= 5/60 × 30⁰
= 2,5⁰
Pergerakan jarum panjang = 5 menit
= 5/60 × 360⁰
= 30⁰
Sudut yang terbentuk = 30 - 2,5⁰
= 27,5⁰
= 27,5⁰ x Ï€/180⁰ Ï€ rad
= 11Ï€/72 rad
Dengan mengikuti langkah diatas maka akan didapatkan jawaban untuk pertanyaan lainnya,
b)11Ï€/24 rad
c) 343Ï€/360 rad
d) 109Ï€/120 rad
e) 61Ï€/120 rad
f) π/4 rad
6. Misalkan θ merupakan sudut lancip dan sudut β adalah sudut tumpul. Perhatikan kombinasi setiap sudut dan kedua sudut tersebut dan tentukan kuadrannya.
a. 3θ
b. 2β
c. θ + β
d. 2β – θ
Jawaban :
a)
θ adalah sudut lancip sehingga θ > 0° dan θ < 90°, maka
3 x 0 < 3 x θ < 3 x 90°
0 < 3θ < 270°
Jadi, 3θ berada di kuadran I,II, atau III.
b)
β adalah sudut tumpul sehingga β > 90° dan β < 180°, maka
2 x 90° < 2 x β < 2 x 180°
180° < 2β < 360°
Jadi, 2β berada di kuadran III atau IV.
c)
sudut lancip + sudut tumpul, maka
0⁰ + 90⁰ < θ + β < 90⁰ + 180⁰
90⁰ < θ + β < 270⁰
Jadi, θ + β berada di kuadran II atau III.
d)
2β – θ, maka
180⁰ - 0⁰ < 2β - θ < 360⁰ - 90⁰
180⁰ < 2β - θ < 270⁰
Jadi, 2β – θ berada di kuadran III.
a)
θ adalah sudut lancip sehingga θ > 0° dan θ < 90°, maka
3 x 0 < 3 x θ < 3 x 90°
0 < 3θ < 270°
Jadi, 3θ berada di kuadran I,II, atau III.
b)
β adalah sudut tumpul sehingga β > 90° dan β < 180°, maka
2 x 90° < 2 x β < 2 x 180°
180° < 2β < 360°
Jadi, 2β berada di kuadran III atau IV.
c)
sudut lancip + sudut tumpul, maka
0⁰ + 90⁰ < θ + β < 90⁰ + 180⁰
90⁰ < θ + β < 270⁰
Jadi, θ + β berada di kuadran II atau III.
d)
2β – θ, maka
180⁰ - 0⁰ < 2β - θ < 360⁰ - 90⁰
180⁰ < 2β - θ < 270⁰
Jadi, 2β – θ berada di kuadran III.
7. Perhatikan pergerakan jarum jam. Berapa kali (jika ada) dalam 1 hari terbentuk sudut-sudut di bawah ini?
a. 90⁰
b. 180⁰
c. 30⁰
d. 120⁰
Jawaban :
Dalam satu hari jarum jam berputar 2x yang menandakan,
00.00 - 11.59 Pagi hingga Siang
12.00 - 23.59 Siang hingga Malam
a)
360⁰/90⁰ x 2 = 8 kali
b)
360⁰/180⁰ x 2 = 3 kali
c)
360⁰/30⁰ x 2 = 24 kali
d)
360⁰/120⁰ x 2 = 6 kali
Dalam satu hari jarum jam berputar 2x yang menandakan,
00.00 - 11.59 Pagi hingga Siang
12.00 - 23.59 Siang hingga Malam
a)
360⁰/90⁰ x 2 = 8 kali
b)
360⁰/180⁰ x 2 = 3 kali
c)
360⁰/30⁰ x 2 = 24 kali
d)
360⁰/120⁰ x 2 = 6 kali
8. Ubahlah sudut-sudut berikut ke bentuk derajat.
Jawaban :
9. Gambarkan setiap ukuran sudut di bawah ini dalam koordinat kartesius.
Jawaban :
*Klik gambar untuk memperbesar*
10. Perhatikan gambar di bawah ini. Selidiki dan tentukan koordinat titik A jika dirotasi sejauh.
Jawaban :
a) Koordinat A setelah dirotasi 90⁰ = (-1/2√3 , 1/2)
b) Koordinat A setelah dirotasi 180⁰ = (-1/2 , -1/2√3)
c) Koordinat A setelah dirotasi 270⁰ = (1/2 , 1/2√3)
d) Koordinat A setelah dirotasi 360⁰ = (1/2 , √3/2)
a) Koordinat A setelah dirotasi 90⁰ = (-1/2√3 , 1/2)
b) Koordinat A setelah dirotasi 180⁰ = (-1/2 , -1/2√3)
c) Koordinat A setelah dirotasi 270⁰ = (1/2 , 1/2√3)
d) Koordinat A setelah dirotasi 360⁰ = (1/2 , √3/2)