Berikut ini merupakan pembahasan kunci jawaban Buku Matematika untuk Kelas 10 halaman 151 Pembahasan kali ini kita akan bahas latihan yang ada pada buku paket MTK Uji Kompetensi 4.3 Halaman 151, 152 Buku siswa untuk Semester 2 (Genap) Kelas X SMP/MTS. Semoga dengan adanya pembahasan kunci jawaban Pilihan Ganda (PG) dan juga Esaay Bab 4 Trigonometri ini, kalian bisa menjadi lebih giat untuk belajar. Kunci jawaban ini diperuntukkan untuk para pelajar yang sedang mengerjakan tugas Kurikulum 2013 (K13). Kunci Jawaban Uji Kompetensi 4.3 Hal 151 Matematika Kls 10
 |
| Kunci Jawaban MTK Kelas 10 Halaman 151 Uji Kompetensi 4.3 |
Kunci Jawaban MTK Kelas 10 Halaman 151 Uji Kompetensi 4.3
Uji Kompetensi 4.3
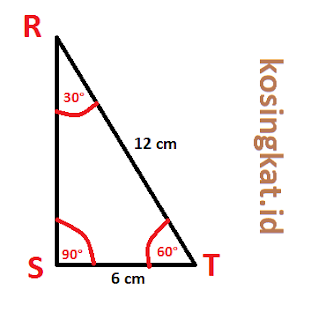
1. Diketahui segitiga RST, dengan ∠S = 90°, ∠T = 60°, dan ST = 6 cm. Hitung:
a. Keliling segitiga RST
b. (sin ∠T)2 + (sin ∠R)2
Jawaban :
a)
R + S + T = 180°
R + 90° + 60° = 180°
R + 150° = 180°
R = 30°
ST = 6 cm (sisi sampingnya 60°)
T = 60°
cos T = samping/miring
cos 60° = 6/TR
1/2 = 6/TR
TR = 12 cm
TR = 12 cm (sisi miringnya)
T = 60°
sin T = depan/miring
sin T = RS / TR
sin 60° = RS / 12
1/2. √3 = RS / 12
RS = [1/2.√3]. 12
RS = 6√3 cm
RS + ST + TR = 6√3 cm + 6 cm + 12 cm
= (18 + 6√3)
= 6(3 + √3) cm
Jadi, keliling segitiga RST adalah 6(3 + √3) cm.
a)
R + S + T = 180°
R + 90° + 60° = 180°
R + 150° = 180°
R = 30°
ST = 6 cm (sisi sampingnya 60°)
T = 60°
cos T = samping/miring
cos 60° = 6/TR
1/2 = 6/TR
TR = 12 cm
TR = 12 cm (sisi miringnya)
T = 60°
sin T = depan/miring
sin T = RS / TR
sin 60° = RS / 12
1/2. √3 = RS / 12
RS = [1/2.√3]. 12
RS = 6√3 cm
RS + ST + TR = 6√3 cm + 6 cm + 12 cm
= (18 + 6√3)
= 6(3 + √3) cm
Jadi, keliling segitiga RST adalah 6(3 + √3) cm.
b)
(sin ∠T)2 + (sin ∠R)2 = (sin 60°)2 + (sin 30°)2
= (1/2 √3)2 + (1/2)2
= 3/4 + 1/4
= 1
Jadi, (sin ∠T)2 + (sin ∠R)2 adalah 1.
2. Hitung nilai dari setiap pernyataan trigonometri berikut.
3. Pilihanlah jawaban yang tepat untuk setiap pernyataan berikut ini. Berikan penjelasan untuk setiap pilihan kamu.
Jawaban :
a. A. sin 60°
b. D. 0
c. A. 0°
d. C. tan 60°
a. A. sin 60°
b. D. 0
c. A. 0°
d. C. tan 60°
4. Jika tan (A + B) = √3, tan (A – B) = 1/√3, dan 0° < A + B ≤ 90°. Tentukan A dan B.
Jawaban :
1/√3= tan 30°
A+B=60
A-B=30
B=15°, A=45°
Jadi, A adalah 45° dan B adalah 15°.
5. Manakah pernyataan yang bernilai benar untuk setiap pernyataan di bawah ini.
a. sin (A + B) = sin A + sin B
b. Nilai sin θ akan bergerak naik pada saat nilai θ juga menaik, untuk 0° ≤ θ ≤ 90°
c. Nilai cos θ akan bergerak naik pada saat nilai θ menurun, untuk 0° ≤ θ ≤ 90°
d. sin θ = cos θ, untuk setiap nilai θ
e. Nilai cot θ tidak terdefinisi pada saat θ = 0°
a. sin (A + B) = sin A + sin B
b. Nilai sin θ akan bergerak naik pada saat nilai θ juga menaik, untuk 0° ≤ θ ≤ 90°
c. Nilai cos θ akan bergerak naik pada saat nilai θ menurun, untuk 0° ≤ θ ≤ 90°
d. sin θ = cos θ, untuk setiap nilai θ
e. Nilai cot θ tidak terdefinisi pada saat θ = 0°
Jawaban :
a. Salah
b. Benar
c. Benar
d. Salah
e. Benar
a. Salah
b. Benar
c. Benar
d. Salah
e. Benar