Kunci Jawaban MTK Kelas 8 Halaman 176 Ayo Kita Berlatih 4.5

Berikut ini merupakan pembahasan kunci jawaban Buku Matematika untuk Kelas 8 halaman 176 Pembahasan kali ini kita akan bahas latihan yang ada pada buku paket MTK Ayo Kita Berlatih 4.5 Halaman 176-177 Buku siswa untuk Semester 1 Kelas VIII SMP/MTS. Semoga dengan adanya pembahasan kunci jawaban Pilihan Ganda (PG) dan juga Esaay Bab 4 Persamaan Garis Lurus Kelas 8 ini, kalian bisa menjadi lebih giat untuk belajar. Kunci jawaban ini diperuntukkan untuk para pelajar yang sedang mengerjakan tugas Kurikulum 2013 (K13). Kunci Jawaban Ayo Kita Berlatih 4.5 Hal 176 Matematika Kls 8

Ayo Kita Berlatih 4.5

1. Tentukan apakah garis berikut sejajar dengan sumbu-X atau sumbu-Y?

Jawaban :

a) Garis p yang melalui A(8, –3) dan B(5, –3). sejajar sumbu-x karena memiliki nilai Y yang sama.
b) Garis q yang melalui C(6, 0) dan D(–2, 0). sejajar sumbu-x karena memiliki nilai Y yang sama.
c) Garis r yang melalui E(–1, 1) dan F(–1, 4). sejajar sumbu-y karena memiliki nilai X yang sama.
d) Garis s yang melalui G(0, 6) dan H(0, –3). berhimpitan sumbu-y karena memiliki nilai X keduanya sama dengan 0.
e) Garis t yang melalui I(2, –4) dan J(–3, –4). sejajar sumbu-x karena memiliki nilai Y yang sama.

2. Tentukan apakah pasangan garis berikut sejajaratau saling tegak lurus?

Jawaban :

a) Gradien garis a = (y2 - y1) / (x2 - x1)
= (3 - (-3)) / (11 - 7)
= (3 + 3) / 4
= 6/4
= 3/2
Gradien garis b = (y2 - y1) / (x2 - x1)
= (6 - 0) / (-5 - (-9))
= 6 / (-5 + 9)
= 6 / 4
= 3/2
Karena gradien garis a = gradien garis b, maka pasangan garis tersebut Saling Sejajar.

b) Gradien garis m = (y2 - y1) / (x2 - x1)
= (0 - 5) / (0 - 3)
= -5 / -3
= 5/3
Gradien garis n = (y2 - y1) / (x2 - x1)
= (3 - 0) / (-5 - 0)
= 3 / -5
= -3/5
Karena gradien garis m jika dikali dengan gradien garis n hasilnya = -1, maka pasangan garis tersebut Saling Tegak Lurus.

3. Kemiringan garis m adalah 2. Tentukan kemiringan garis n jika:

Jawaban :

a) Gradien m = 2 sejajar dengan garis n, karena sejajar maka :
Gradien n = gradien m = 2
Jadi, kemiringan garis n adalah 2.

b) Gradien m = 2 tegak lurus dengan garis n, karena tegak lurus maka :
Gradien n = -1 / gradien m = -1/2
Jadi, kemiringan garis n adalah -1/2.

4. Diketahui sebuah garis lurus memiliki persamaan y = 2x + 5.

Jawaban :

Gradien garis y = 2x + 5, y = mx + c, maka m1 = 2.

a) y = 2x - 8,
y = mx + c
m2 = 2
karena m1 = m2 = 2, maka Sejajar

b) 4x - 2y + 6 = 0
a = 4, b = -1, c = 0
m2 = -a/b = -4/-2 = 2
karena m1 = m2 = 2, maka Sejajar

c) 3y = 6x – 1
6x -3y - 1 = 0
a = 6, b = -3, c = -1
m2 = -a/b = -6/-3 = 2
karena m1 = m2 = 2, maka Sejajar

d) 7x – 14y + 2 = 0
a = 7, b = -14, c = 2
m2 = -a/b = -7/-14 = 1/2
karena m1 x m2 = 2 x 1/2 = 1, maka Tidak Tegak Lurus ataupun Sejajar

5. Coba buktikan apakah persamaan garis lurus berikut saling tegak lurus.

Jawaban :

a) 2y = 2x – 3
y = x -3/2
y = mx + c
m1 = 1

y = –x + 3
y = mx + c
m2 = –1
Karena m1 x m2 = 1 x -1 = -1, maka kedua garis Saling Tegak Lurus

b) 3x + y = 7
y = -3x + 7
y = mx + c
m1 = -3

3x – 6y = 7
6y = 3x - 7
y = 1/2x -7/6
m2 = 1/2
Karena m1 x m2 tidak sama dengan -1, maka kedua garis Tidak Saling Tegak Lurus

c) (4x + 6)/3 = 4y
12y = 4x + 6
y = 1/3x + 1/2
y = mx + c
m1 = 1/3

3x + 4y + 2 = 0
a = 3, b = 4, c = 2
m2 = -a/b = -3/4
Karena m1 x m2 tidak sama dengan -1, maka kedua garis Tidak Saling Tegak Lurus

6. Diketahui persamaan garis lurus 3x + 4y – 5 = 0 dan 6x + 8y – 10 = 0.

Jawaban :

Gradien garis 3x + 4y - 5 = 0 :
a = 3, b = 4, c = -5
m1 = -a/b = -3/4

Gradien garis 6x + 8y - 10 = 0
a = 6, b = 8, c = -10
m2 = -a/b = -6/8 = -3/4

Karena m1 = m2, maka kedudukan dua persamaan garis tersebut adalah Saling Sejajar.

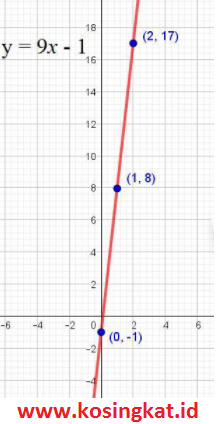
7. Diketahui fungsi f(x) = 3x + 7 dan g(x) = 6x – 8. Bagaimanakah kedudukan dari dua fungsi tersebut?

Jawaban :

f(x) = 3x + 7
m1 = 3

g(x) = 6x - 8
m2 = 6
Karena m1 tidak sama dengan m2, maka kedudukan dua fungsi tersebut adalah Saling Berpotongan.

Grafik f(x) + g(x)
y = f(x) + g(x)
y = 3x + 7 + 6x – 8
y = 9x - 1

Titik yang dilalui (0,-1) , (1,8) , (2,17)

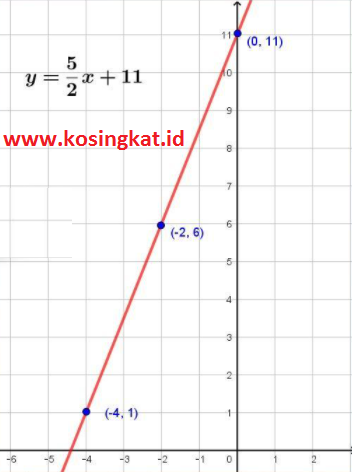
8. Diketahui fungsi f(x) = 2x + 5 dan g(x) = –1/2 x – 6. Bagaimanakah kedudukan dari dua fungsi tersebut?

Jawaban :

f(x) = 2x + 5
m1 = 2
g(x) = -1/2x - 6
m2 = -1/2

Karena m1 x m2 = 2 x -1/2 = -1, maka kedudukan dari dua fungsi tersebut adalah Saling Tegak Lurus

Grafik f(x) - g(x)
y = f(x) - g(x)
y = 2x + 5 - (-1/2x - 6)
y = 2x + 5 + 1/2x + 6
y = 5/2x + 11

Titik yg dilalui (-4,1) , (-2,6) , (0,11)

Kunci Jawaban MTK Kelas 8 Halaman 176 Ayo Kita Berlatih 4.5

Kunci Jawaban MTK Kelas 8 Halaman 176 Ayo Kita Berlatih 4.5

Ayo Kita Berlatih 4.5

Related Posts