Berikut ini merupakan pembahasan kunci jawaban Buku Matematika untuk Kelas 9 halaman 226 Pembahasan kali ini kita akan bahas latihan yang ada pada buku paket MTK Latihan 4.2 Halaman 226-228 Buku siswa untuk Semester 1 (Ganjil) Kelas IX SMP/MTS. Semoga dengan adanya pembahasan kunci jawaban Pilihan Ganda (PG) dan juga Esaay Bab 4 Kekongruenan dan Kesebangunan Kelas 9 ini, kalian bisa menjadi lebih giat untuk belajar. Kunci jawaban ini diperuntukkan untuk para pelajar yang sedang mengerjakan tugas Kurikulum 2013 (K13). Kunci Jawaban Latihan 4.2 Hal 226 Matematika Kls 9
 |
| Kunci Jawaban MTK Kelas 9 Halaman 226 Latihan 4.2 |
Kunci Jawaban MTK Kelas 9 Halaman 226 Latihan 4.2
Latihan 4.2 Kekongruenan Dua Segitiga
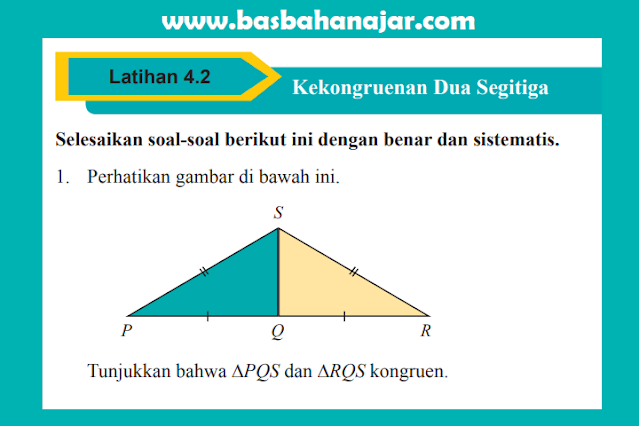
1. Perhatikan gambar di bawah ini. Tunjukkan bahwa ∆PQS dan ∆RQS kongruen.
Jawaban :
- PQ = RQ (diketahui pada gambar)
- QS (pada ΔPQS) = QS (pada ΔRQS)
- PS = RS (diketahui pada gambar)
Jadi, ΔPQS dan ΔRQS kongruen berdasarkan kriteria sisi – sisi – sisi.
- PQ = RQ (diketahui pada gambar)
- QS (pada ΔPQS) = QS (pada ΔRQS)
- PS = RS (diketahui pada gambar)
Jadi, ΔPQS dan ΔRQS kongruen berdasarkan kriteria sisi – sisi – sisi.
2. Perhatikan gambar di bawah ini. Panjang AB = DE dan AB//DE. Tunjukkan bahwa ∆ABC dan ∆EDC kongruen.
Jawaban :
AB = DE
∠ DCE = ∠ ACB (bertolak belakang)
∠ ABC = ∠ CDE (berseberangan)
Jadi, ΔABC dan ΔCDE kongruen berdasarkan kriteria sisi, sudut, sudut.
AB = DE
∠ DCE = ∠ ACB (bertolak belakang)
∠ ABC = ∠ CDE (berseberangan)
Jadi, ΔABC dan ΔCDE kongruen berdasarkan kriteria sisi, sudut, sudut.
3. Titik C adalah titik pusat lingkaran. Tunjukkan bahwa dua segitiga pada gambar di samping adalah kongruen.
Jawaban :
CA = CB = jari-jari lingkaran
m∠ACB = m∠ECD (bertolak belakang)
CD = CE = jari-jari lingkaran
Jadi, ΔACB dan ΔECD kongruen berdasarkan kriteria sisi – sudut – sisi.
CA = CB = jari-jari lingkaran
m∠ACB = m∠ECD (bertolak belakang)
CD = CE = jari-jari lingkaran
Jadi, ΔACB dan ΔECD kongruen berdasarkan kriteria sisi – sudut – sisi.
4. Bangun WXYZ adalah segi empat dengan sisi-sisi yang berhadapan panjangnya sama. XZ adalah salah satu diagonalnya.
Jawaban :
a) WZ = XY, WX = ZY, ZX = XZ. Jadi, ΔWXZ dan ΔZYX. kongruen berdasarkan kriteria sisi - sisi - sisi.
b) Karena ΔWXZ dan ΔZYX kongruen, maka ketika digabungkan bangun WXYZ merupakan sebuah Jajargenjang.
a) WZ = XY, WX = ZY, ZX = XZ. Jadi, ΔWXZ dan ΔZYX. kongruen berdasarkan kriteria sisi - sisi - sisi.
b) Karena ΔWXZ dan ΔZYX kongruen, maka ketika digabungkan bangun WXYZ merupakan sebuah Jajargenjang.
5. Perhatikan gambar di bawah ini. Titik O adalah pusat lingkaran dalam dan lingkaran luar.
Jawaban :
OA = OB adalah jari-jari lingkaran (sisi diketahui)
∠ OAP = ∠ OBP (sudut diketahui)
∠ OPB = ∠ OPA adalah sudut siku-siku (sudut diketahui)
Jadi, titik P adalah titik tengah AB.
OA = OB adalah jari-jari lingkaran (sisi diketahui)
∠ OAP = ∠ OBP (sudut diketahui)
∠ OPB = ∠ OPA adalah sudut siku-siku (sudut diketahui)
Jadi, titik P adalah titik tengah AB.
6. Perhatikan gambar di bawah ini. Pada segitiga ABC, BM tegak lurus dengan AC, CN tegak lurus dengan AB. Panjang BM = CN.
Jawaban :
BM = CN (diketahui)
BC = BC (berhimpit)
m∠BMC = m∠CNB = 90° (diketahui)
Jadi, ΔBCM kongruen dengan ΔCBN.
BM = CN (diketahui)
BC = BC (berhimpit)
m∠BMC = m∠CNB = 90° (diketahui)
Jadi, ΔBCM kongruen dengan ΔCBN.
7. Perhatikan gambar di bawah ini. Titik M adalah titik tengah QR. Garis XM dan YM masing-masing tegak lurus pada PQ dan PR.
Jawaban :
QM = MR (sisi diketahui)
∠ MXQ = ∠ MYR (sudut diketahui sudut siku-siku)
∠ XMQ = ∠ YMR (diketahui sudut berimpit/beradu)
Jadi, ΔQMX dan ΔRMY kongruen berdasarkan kriteria sisi - sudut - sudut.
QM = MR (sisi diketahui)
∠ MXQ = ∠ MYR (sudut diketahui sudut siku-siku)
∠ XMQ = ∠ YMR (diketahui sudut berimpit/beradu)
Jadi, ΔQMX dan ΔRMY kongruen berdasarkan kriteria sisi - sudut - sudut.
8. Menalar. Diketahui SR//PQ, OP = OQ, OS = OR. Ada berapa pasang segitiga yang kongruen? Sebutkan dan buktikan.
Jawaban : Ada 3 pasang segitiga kongruen yaitu: ΔPOS dengan ΔQOR, ΔPSR dengan ΔQRS, dan ΔPSQ dengan ΔQRP.
9. Berpikir Kritis. Apakah dua segitiga yang mempunyai tiga pasang sudut-sudut yang bersesuaian sama besar pasti kongruen?
Jawaban :
Belum tentu, tiga pasang sudut yang bersesuaian sama besar belum menjamin dua segitiga tersebut kongruen. Misal, ada 2 segitiga sama sisi, yang memiliki panjang sisi yang berbeda misal a dan b. Tetapi kedua segitiga tersebut bisa saja tidak kongruen karena memiliki panjang sisi yang berbeda atau luas yang berbeda.
Belum tentu, tiga pasang sudut yang bersesuaian sama besar belum menjamin dua segitiga tersebut kongruen. Misal, ada 2 segitiga sama sisi, yang memiliki panjang sisi yang berbeda misal a dan b. Tetapi kedua segitiga tersebut bisa saja tidak kongruen karena memiliki panjang sisi yang berbeda atau luas yang berbeda.
10.
Berpikir Kritis. Apakah dua segitiga yang mempunyai dua pasang sisi
yang bersesuaian sama panjang dan sepasang sudut yang bersesuaian sama
besar pasti kongruen?
Jawaban :
Belum tentu, Kecuali dua sisi yang bersesuaian sama panjang yang mengapit satu sudut yang diketahui sama besar (kriteria sisi – sudut – sisi).
Belum tentu, Kecuali dua sisi yang bersesuaian sama panjang yang mengapit satu sudut yang diketahui sama besar (kriteria sisi – sudut – sisi).
12. Mengukur Panjang Danau Chan ingin mengukur panjang sebuah danau tetapi tidak memungkinkan mengukurnya secara langsung.
Jawaban :
Strategi Chan benar. Dia menggunakan konsep dua segitiga kongruen. ΔPQR dijamin sebangun dengan ΔPQ'R' karena memenuhi kriteria kekongruenan dua segitiga sisi – sudut – sisi, yaitu:
PQ = PQ' (diketahui)
m∠QPR = m∠Q'PR’' (bertolak belakang)
PR = PR' (diketahui)
Jadi, panjang danau QR = Q'R'.
Strategi Chan benar. Dia menggunakan konsep dua segitiga kongruen. ΔPQR dijamin sebangun dengan ΔPQ'R' karena memenuhi kriteria kekongruenan dua segitiga sisi – sudut – sisi, yaitu:
PQ = PQ' (diketahui)
m∠QPR = m∠Q'PR’' (bertolak belakang)
PR = PR' (diketahui)
Jadi, panjang danau QR = Q'R'.

