Kunci Jawaban MTK Kelas 12 Halaman 12 Soal Latihan 1.1

Halo gaes kembali lagi diwebsite saya, pada pembahasan kali ini saya akan membagikan sebuah kunci jawaban yang akan memudahkan teman-teman dalam mengerjakan tugas sekolah. Nah pada artikel kali ini saya akan bahas pelajaran Matematika atau MTK.

Untuk tingkat atau jenjangnya yaitu untuk Kelas XII SMA/MA/SMK/MAK untuk ketentuan bukunya, soal-soal yang akan saya bahas kunci jawabannya ini terdapat dalam Buku Kemdikbud Kurikulum 2013 Revisi tahun 2018.

Secara detailnya, saya akan bahas Kunci Jawaban Matematika Kelas 12 Halaman 12 Soal Latihan 1.1 dan terdapat pada Bab 1 Dimensi 3. Semoga dengan adanya artikel seputar kunci jawaban ini bisa membantu teman-teman atau siswa-siswa dalam mengerjakan Tugas Sekolah dan membantu para guru dalam memberikan pelajaran kepada muridnya.

Kunci Jawaban MTK Kelas 12 Halaman 12 Soal Latihan 1.1

Disclaimer : Kunci Jawaban yang saya tulis diwebsite ini tidak menjadi patokan pasti benar, saya hanya membantu dan silahkan cek lagi apabila jawaban yang saya berikan kurang memuaskan

Pembahasan :

1. Diketahui limas beraturan T.ABC dengan bidang alas berbentuk segitiga
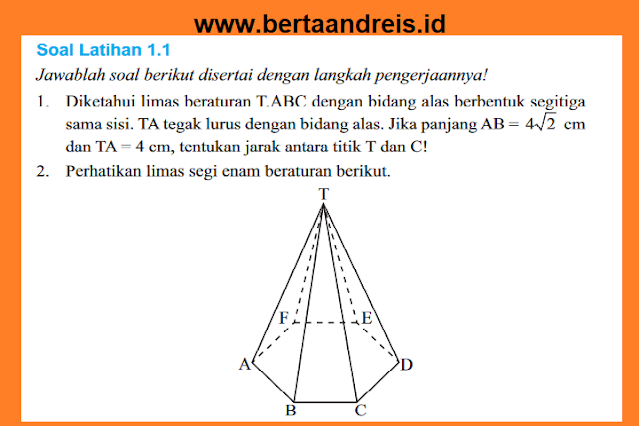
sama sisi. TA tegak lurus dengan bidang alas. Jika panjang AB = 4 cm dan TA = 4 cm, tentukan jarak antara titik T dan C!

Jawab:
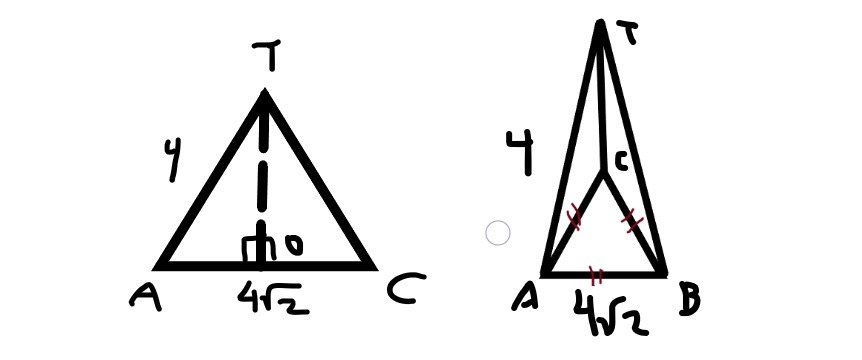
Dik: limas T.ABC alas segitiga sama sisi,
TA tegak lurus bidang alas.
AB = 4(2)^1/2 cm dengan TA = 4cm,
Dit: TC = ?

$4 = \sqrt{ 2\sqrt{2}^{2} + TO^{2} } \\ 16 = 8 + TO^{2} \\ TO = \sqrt{8} \\ TO = 2\sqrt{2}$

$TC = \sqrt{\frac{AC}{2}^{2} + TO^{2}} \\ TC = \sqrt{2\sqrt{2}^{2} + (2\sqrt{2}^{2}) } \\ TC = \sqrt{8 + 8} \\ TC = 4 cm$

2. Perhatikan limas segi enam beraturan berikut

Diketahui panjang AB = 10 cm dan TA = 13 cm. Titik O merupakan titik tengah garis BE. Tentukan jarak antara titik T dan O!

Jawab:

Dik: limas segienam T.ABCDEF
AB = 10 cm
TA = 13 cm .
Titik O merupakan titik tengah garis BE .
Dit : jarak antara titik T dan O :
perhatikan alas limasnya, alas limas berbentuk segi 6 beraturan, jika kita ambil 1 segitiga akan membentuk segitiga sama sisi,
sehingga BO = AB = 10 cm
TB = TA = 13 cm

perhatikan segitiga BTO
segitiga BTO segitiga siku" di O
segingga panjang TO bisa kita hitung dengan menggunakan pythagoras

TO = √(13² - 10²)
= √(169 - 100)
= √69 cm

jadi jarak antara titik T ke titik O = √69 cm

3. Perhatikan bangun berikut ini.

Jawaban :
a. Jarak antara titik A dan C
Jawab: AC = √(AB² + BC²)
AC = √(5² + 4²)
AC = √(25 + 16)
AC = √41 cm

b. Jarak antara titik E dan C
Jawab: EC = √(AE² + AC²)
EC = √(4² + (√41)²)
EC = √(16 + 41)
EC = √57 cm

c. Jarak antara titik A dan G
Jawab: Tentukan panjang EG terlebih dahulu
EG = √(AB² + FG²)
EG = √(4² + 4²)
EG = √(16 + 16)
EG = √(32)
EG = √(16 . 2)
EG = 4√2 cm

Tentukan panjang AG
AG = √(AE² + EG²)
AG = √(4² + (4√2)²)
AG = √(16 + 32)
AG = √(48)
AG = √(16 . 3)
AG = 4√3 cm

Penutup

yak itulah tadi pembahasan Kunci Jawaban MTK Kelas 12 Halaman 12 Soal Latihan 1.1. Jika sekiranya ada yang kurang jelas ataupun keliru, silahkan teman-teman berikan komentarnya dibawah. Dan mungkin sekiranya artikel ini membantu, silahkan teman-teman bagikan artikel ini lewat whatsapp, instagram, facebook dan lain-lain.

Kunci Jawaban MTK Kelas 12 Halaman 12 Soal Latihan 1.1