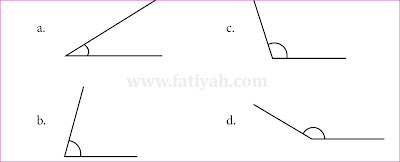
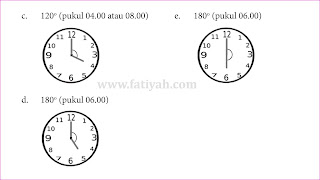
Kunci Jawaban MTK Kelas 4 Halaman 185 Ayo Mencoba
Berikut ini merupakan pembahasan kunci jawaban Buku Senang Belajar Matematika untuk Kelas 4 halaman 185 Pembahasan kali ini kita akan bahas latihan yang ada pada buku paket MTK Ayo Mencoba Halaman 185 Buku siswa untuk Semester 2 Kelas IV SD/MI. Semoga dengan adanya pembahasan kunci jawaban Pilihan Ganda (PG) dan juga Esaay Bab 6 Pengukuran Sudut ini, kalian bisa menjadi lebih giat untuk belajar. Kunci jawaban ini diperuntukkan untuk para pelajar yang sedang mengerjakan tugas Kurikulum 2013 (K13 Revisi 2018). Kunci Jawaban Matematika Kls 4 Hal 185 Ayo Mencoba
 |
| Kunci Jawaban MTK Kelas 4 Halaman 185 Ayo Mencoba |