Jawaban Latihan 4.1.1 Bab 4 MTK Kelas 12 Halaman 187 (Diagonal Dan Penerapannya)
Bab 4 (Diagonal Bidang, Diagonal Ruang, Bidang Diagonal, Dan Penerapannya)
Latihan 4.1.1
Halaman 187-192
Matematika (MTK)
Kelas 12 (XII) SMA/SMK/MAK
Semester 2 K13
1. Isilah tabel berikut ini dengan tanda centang ( √ )
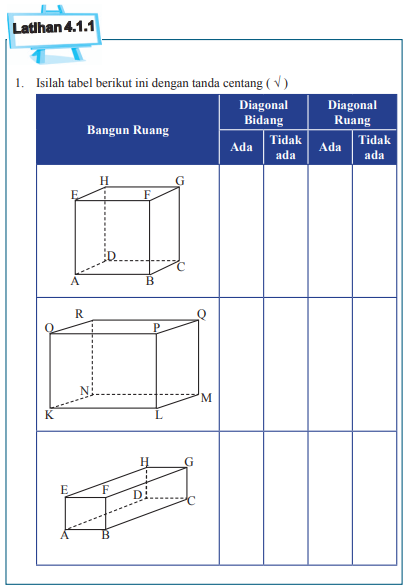 |
| Gambar Latihan 4.1.1 Halaman 187 “Kubus Sampai Tabung” |
Jawab:
a.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
b.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
c.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
d.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
e.
>> Diagonal Ruang:
Tidak ada
>> Diagonal Bidang:
Ada
f.
>> Diagonal Ruang:
Tidak ada
>> Diagonal Bidang:
Ada
g.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
h.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
i.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
j.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Ada
k.
>> Diagonal Ruang:
Ada
>> Diagonal Bidang:
Tidak Ada
_________________________________
2.
a. Pada Gambar 1, jika diketahui panjang AB = BC = CG = 4 cm, JK
= 3 cm, dan BJ = 1 cm hitunglah panjang AC, AK, dan LG.
b. Pada Gambar 2, jika diketahui panjang AB=5 cm, AE=BC=EF= 4 cm hitunglah panjang AC, EG, DF, dan AG.
Jawab:
a. Gambar 1
AC = 4√2 karena diagonal persegi
diketahui
BK’ = 3
AK’ = √AB² + BK’²
= √4² + 3²
= √16 + 9
= √25
= 5
KK’ = 1 cm
AK = √AK’² + KK’²
= √5² + 1²
= √25 + 1
= √26
LF = √LE²²+ EF²
LF = √3² + 4²
LF = √9 + 16
= √25
= 5
FG = 1 cm
LG = √LF² + FG²
= √5² + 1²
= √25 + 1
= √26
b. Gambar2
AC²= (AB²+BC²)
AC =√52 + 42
AC = √25 +16
AC = √41 cm
EC²=AC²+AE²
EC=√(√41) ²+ 4²
EC =√(41+16)
EC = √57
AG2= (AJ ² + GJ²)
AG =√(4²+4²)
AG = √(16+16)
AG = √32
AG = √16 x √2
AG = 4√2
_________________________________
3. Perhatikan aquarium berikut ini.
Pada akuarium tersebut akan ditambahi hiasan yang digantungkan pada kawat yang dipasang di dalam aquarium melintang dari ujung atas ke ujung bawah. Tentukan panjang kawat yang diperlukan!
Jawab:
P = 6 ft
t = 4 ft
l = 2,5 ft
panjang kawat = 4 (p + t + l)
= 4 (6 + 4 + 2,5) ft
= 4 × 12,5 ft
= 50 ft (kaki)
________________________________
4. Dari gambar di samping, jika diketahui panjang AB = 8 cm, BC = 6 cm dan EC = 5√5 berapakah luas segitiga AEC dan ABC?
Jawab:
titik E adalah titik tengah garis AB, shg:
Luas Δ ABC = 1/2 x a x t
= 1/2 x 8 x 5√5
= 20√5 cm²
dan,
Luas Δ AEC = 1/2 x a x t
= 1/2 x 4 x 5√5
= 10√5 cm²
________________________________
5. Ani akan membuat kerangka suatu balok seperti gambar berikut.
Jika panjang KL = 5 cm, LM = 10 cm, dan LR = 5√6 cm, maka berapa kawat yang dibutuhkan Ani untuk membuat kerangka balok tersebut?
Jawab:
Karena baloknya adalah KLMN.OPQR
Panjang = 5 cm
Lebar = 10 cm
Diagonal ruang = 5√6 cm
Berlaku:
Dengan tinggi = 5 cm
Maka panjang kawat yang diperlukan adalah:
________________________________
6. Diketahui limas T.ABCD dengan alas berbentuk persegi seperti berikut.
Panjang BD=12√2 cm dan TO = 8 cm. Tentukan
a. Luas segitiga TBC
b. Volume limas T. ABCD
Jawab:
________________________________
7. Suatu kepanitian membuat papan nama dari kertas yang membentuk bangun seperti berikut.
Ternyata ABE membentuk segitiga sama sisi, panjang BF = 13 cm dan BC = 12 cm. Berapakah ukuran kertas yang digunakan untuk membuat papan nama tersebut?
Jawab:
tinggi prisma = √(13² – 12²)
= √(169 – 144)
= √25 cm
= 5 cm
Cari Luas alas:
L Δ ABC = 1/2.a.t
= 1/2 . 12 . [√(12²-6²)]
= 6 . 10,4
= 62,4 cm²
Next, bisa dihitung luas permukaan prisma.
L permukaan prisma adalah = 2 x luas alas + luas selubung
= 2 x 62,4 + 3 x (5 . 12)
= 124,8 + 180
= 304,8 cm²
Jadi ukuran kertas yang digunakan adalah 304,8 cm²
________________________________
8. Balok dengan panjang diagonal ruang 20√2 cm. Rusuk-rusuk balok tersebut bertemu pada suatu titik sudut dengan perbandingan 3 : 4 : 5. Berapa rusuk terpanjang dari balok tersebut?
Jawab:
DR = √ (P² + L² + T²)
20√2 = √ ((3n)² + (4n)² + (5n)² )
(20√2)² = 9n² + 16n² + 25n²
800 = 50n²
n² = 800/50 = 16
n = √16 = 4
Rusuk terpanjang = 5n
= 5(4)
= 20 cm
________________________________
9. Luas permukaan suatu kubus adalah 294 cm2. Tentukan
a. Panjang diagonal bidangnya
b. Panjang diagonal ruangnya
c. Volume kubus
Jawab:
luas permuakaan kubus = 6 x s² ——> inii rumusnya
294 = 6s²
s² = 49
s = √49
s = 7
a. diagonal bidang = s√2 —->ini rumusnya
= 7√2
b. diagonal ruang = s√3 —–> ini rumusnya
= 7√3
c. vollume = s³ = 7³ = 343
________________________________
10. Tentukan banyaknya diagonal bidang dan diagonal ruang pada bangun ruang berikut.
a. Prisma segilima
b. Prisma segidelapan
Jawab:
a. Prisma segilima
Diagonal bidang
d = n (n – 1)
d = 5(5-1)
= 5(4)
= 20
diagonal ruang
d = n (n – 3)
= 5 ( 5-3)
= 5 ( 2)
= 10
b. Prisma segidelapan
d = n (n – 1)
d = 8(8-1)
= 8(7)
=56
diagonal ruang
d = 8 (8 – 3)
= 8 ( 8-3)
= 8 ( 5)
= 40
________________________________
11. Suatu kubus panjang diagonal ruangnya adalah a cm. tentukan:
a. Panjang rusuk kubus tersebut
b. Panjang diagonal bidang kubus tersebut
Jawab:
a.
diagonal ruang = s√3
a = s√3
s =
s = .a.√3
b.
diagonal bidang = s√2
= .a.√3 .√2
= a√6
________________________________